16.4. The inner orbital structure of elliptical galaxies¶
To better understand the internal structure of elliptical galaxies and their stellar populations, SAURON was followed by the larger, statistical ATLAS\(^{\mathrm{3D}}\) survey (Cappellari et al. 2011). The ATLAS\(^{\mathrm{3D}}\) survey is statistical in the sense that it selects a sample of galaxies for detailed integral-field spectroscopy based on a simple combination of selection criteria applied to a complete parent sample of galaxies. Briefly, the ATLAS\(^{\mathrm{3D}}\) survey consists of all early-type galaxies (elliptical and lenticular) within 42 Mpc that are observable from the William Herschel Telescope on La Palma, are away from the Milky Way’s mid-plane, and that have an absolute 2MASS \(K_s\) band magnitude \(M_K < -21.5\) (corresponding to a stellar mass \(M_* \gtrsim 6\times 10^9\,M_\odot\)). These selection criteria give 871 galaxies, with 192 lenticular galaxies (22 percent) and 68 elliptical galaxies (8 percent; we will again simply refer to all of these as “elliptical galaxies”); only the elliptical and lenticular galaxies were followed up with IFS observations.
As with the SAURON sample, it is instructive to first simply consider the kinematic maps to get a sense of the range of kinematic behavior among elliptical galaxies. Because the ATLAS\(^{\mathrm{3D}}\) sample is statistical, we can now quantitatively determine the occurrence of different types of kinematics. Krajnovic et al. (2011) did this by applying a method, kinemetry, to the mean line-of-sight velocity maps. Kinemetry is similar to the method discussed in Chapter 12.1 to determine whether an elliptical galaxy is boxy or disky, in that one fits elliptical profiles to the kinematic map and then determines whether higher-order harmonics are present in the kinematics or not. This is motivated by the fact that many elliptical galaxies display rotation signatures (see Section 16.2), for which the expected line-of-sight velocity is \(V(x,y) = V_0 + v_\phi(R)\,\cos\theta\,\sin i\); we derived this relation for a thin disk in circular rotation in Chapter 8.1.2 (see Equation 8.2), but allow here for a rotation velocity \(v_\phi\) that is different from the circular velocity, because the rotation speed in elliptical galaxies is much less than the circular velocity. By fitting the parameters of this basic form (the ellipse’s center, \(\cos i\), and the position angle of the major axis at the receding-velocity side, known as the kinematic position angle), we can determine how regular the rotation pattern of a given galaxy is.
Deviations from simple rotation can come in different forms: smooth or abrupt changes in the kinematic position angle, multiple maxima in \(v_\phi(R)\), or an absence of clear rotation (parameterized through the relative strength \(k_5/k_1\) of the amplitude of the \(\sin (5\theta)\) and \(\cos (5 \theta)\) terms, \(k_5\), with respect to \(k_1 = v_\phi(R)\,\sin i\)). Krajnovic et al. (2011) classify galaxies with average \(k_5/k_1 < 0.04\) as regular rotators (RR), while other galaxies are non-regular rotators (NRR). Abrupt changes in the kinematic position angle are associated with a kinematically-decoupled core (KDC) or even a counter-rotating core (CDC; when the position angle changes by \(180^\circ\)), while smooth changes in position angle are kinematic twists (KT). Galaxies with no deviations are classified as “no feature” (NF), while those with simply very small rotational velocities have “low velocity” (\(k_1 < 5\,\mathrm{km\,s}^{-1}\)), and those with two maxima as “2M”. Finally, some galaxies have multiple peaks in their velocity dispersion and are denoted by “\(2\sigma\)”. Examples of the way that these different kinematic features manifest themselves in ATLAS\(^{\mathrm{3D}}\) galaxies are given in the Figure 16.8, where the black lines are contours of the photometric observations.
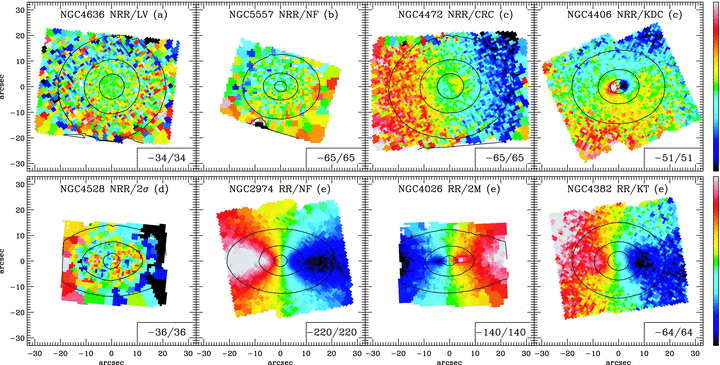
Figure 16.8: Examples of kinematic features found for ATLAS\(^{\mathrm{3D}}\) galaxies (Krajnovic et al. 2011).
From looking at all 260 ATLAS\(^{\mathrm{3D}}\) galaxies and considering the way in which the various kinematic features appear and correlate with each other, Krajnovic et al. (2011) divided the sample in five kinematic groups with some galaxies being unclassified. In Figure 16.9, these are: (a) NRR/LV, (b) NRR/NF; (c) KDC or CRC, (d) \(2\sigma\), (e) RR/NF, RR/2M, RR/KT, (f) unclassified (U). Approximately 80% of the galaxies has regular rotation or is close to it (meaning that the galaxy is a regular rotator with either no feature, two \(v_\phi\) maxima, or a smooth kinematic twist). Another \(\approx 7\%\) have a kinematically-decoupled core or a counter-rotating core, and a further \(\approx4\%\) are characterized by multiple dispersion peaks. Finally, \(\approx 7\%\) of galaxies are non-regular rotators with either low velocity or no feature. The various statistics on the kinematics of elliptical galaxies are shown in Figure 16.9.
Figure 16.9: Kinematic classification of elliptical galaxies (Krajnovic et al. 2011). Left: regular rotator vs. non-regular rotator. Middle: prevalence of different kinemetric features (see Figure 16.8). Right; fraction of different kinematic groups.
Thus, one of the main take-aways from this detailed look at the kinematics of elliptical galaxies is that \(\approx 80\%\) of them have quite regular rotation. The remaining \(20\%\) have complex kinematics that is indicative of a complex orbital structure that is likely triaxial. Dynamical modeling of the latter group requires Schwarzschild modeling to deal with the complexity of the observed kinematics, but for the former group that makes up the vast majority of the sample, the simpler JAM modeling from the previous section suffices (as shown by comparing JAM and Schwarzschild models for galaxies of this type; Cappellari 2008).
The detailed IFS observations of elliptical galaxies by SAURON and ATLAS\(^{\mathrm{3D}}\) also lets us reconsider the question of how much of the shape of the elliptical galaxies is due to rotational flattening versus anisotropic random motions. We first discussed this in Chapter 14.2, where we concluded that the flattened, oblate shapes of elliptical galaxies cannot solely be due to rotational flattening of an isotropic rotator, because the observed rotation velocities are too small to support the oblate shape. The next simplest model is that of an anisotropic rotator, where the velocity dispersion is smaller in the direction along which the density is flattened, which we’ll take to be the \(z\) axis. In terms of the contribution to the kinetic energy tensor from random motions, \(\vec{\Pi}_{\alpha\beta}\) (see Equation 14.14), this means that \(\Pi_{zz} < \Pi_{RR}\) or that the following anisotropy parameter \begin{equation}\label{eq-ellipmass-anisotropybetaz-kintensor} \beta_z \equiv 1-{\Pi_{zz} \over\Pi_{RR}}\,, \end{equation} is larger than zero. Note that this definition is similar to that of \(\beta_z\) in JAM models, Equation (16.8); indeed, under the JAM assumption of constant \(\sigma_z\) and \(\sigma_R\), the two are equal. But the advantage of the definition from Equation (16.14) is that it can be computed for Schwarzschild models as well.
With full dynamical models, we can turn the \(v/\sigma\) versus ellipticity diagram that we discussed in Chapter 14.2 into a similar anisotropy \(\beta_z\) versus intrinsic ellipticity diagram that contains direct information on the orbital structure of galaxies. This is shown for a set of Schwarzschild and JAM models in Figure 16.10.
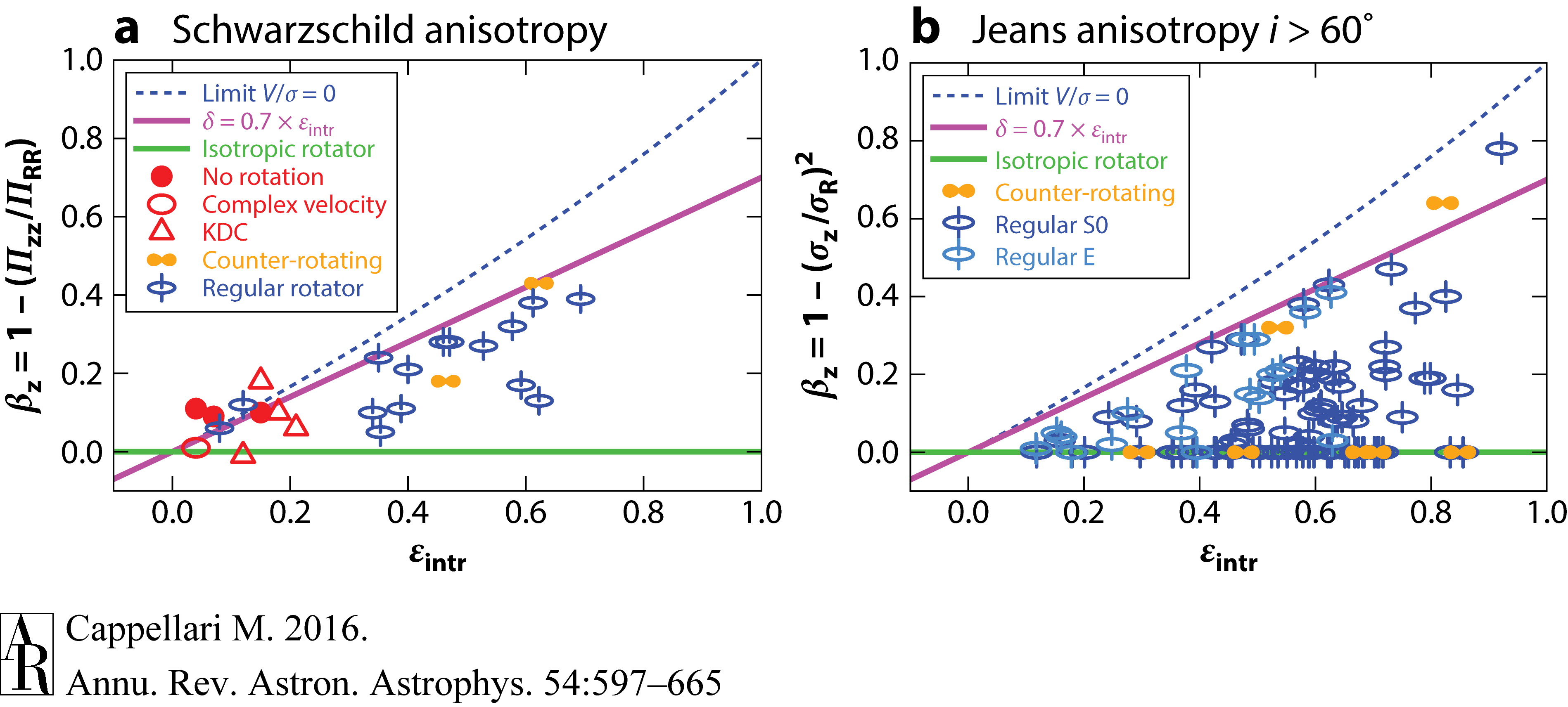
Figure 16.10: Orbital anisotropy vs. ellipticity for elliptical galaxies (Cappellari 2016). Schwarzschild modeling of the orbital structure is employed in the left panel, while the right panel results are obtained using simpler JAM models.
The first thing to notice is the similarity between the diagram obtained with Schwarzschild modeling and that with the simpler JAM models. This is another indication that JAM models suffice to capture the main behavior of the dynamics of a wide range of elliptical galaxies. The dashed line shows the locus of galaxies that are entirely supported by an anisotropic velocity dispersion and have no rotation. All galaxies that are significantly flattened, \(\varepsilon \gtrsim 0.3\), lie well below this line and there seems to be an upper limit to their anisotropy given by the purple line. We also see that the regular rotators are the only elliptical galaxies that are significantly flattened intrinsically and that they are by and large quite anisotropic, although the JAM models show that a subset of them can be explained as pure isotropic rotators. Galaxies without a clear rotation pattern are generally close to round and they require therefore little anisotropy to support their shapes. However, the left panel also demonstrates that these are the galaxies with complex kinematics and kinematically-decoupled cores, indicating that they are most likely triaxial.
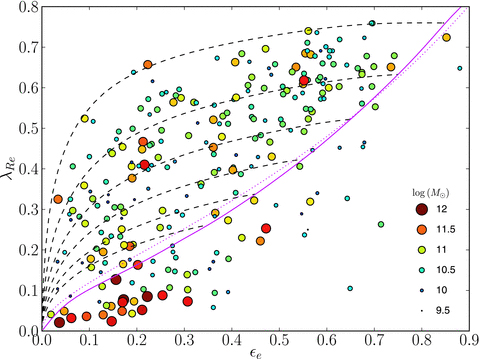
Finally, we can introduce one more useful quantity to characterize the dynamical structure of elliptical galaxies, a proxy for the projected specific angular momentum of stars in the galaxy defined as (Emsellem et al. 2007) \begin{equation} \lambda_R = {\langle R|V|\rangle \over \langle R\sqrt{V^2+\sigma^2}\rangle}\,, \end{equation}
|
|
Figure 16.11: Projected specific angular momentum \(\lambda_{R_e}\) within the effective radius vs. ellipticity (left: Emsellem et al. 2011; right; Cappellari 2016).
Comparing these figures to the orbital anisotropy vs. ellipticity in Figure 16.10 above, it is clear that \(\lambda_{R_e}\) is able to separate the dynamically-distinct regular rotators and non-regular rotators very well, without requiring any dynamical modeling.
The results discussed in this and the previous sections therefore clearly show that there are two distinct classes of elliptical galaxies in the present-day Universe. On the one hand there are the fast rotators that display regular rotation fields that can be well modeled as anisotropic, axisymmetric rotators that are in many ways simply puffed-up disks. Figure 16.11 demonstrates that fast rotators dominate the elliptical-galaxy population at the lower stellar-mass end of \(M_* \lesssim 2 \times 10^{11}\,M_\odot\). The right-hand panel furthermore demonstrates that the fast rotators almost entirely encompass the population of power-law galaxies, those galaxies with power-law inner density profiles. While the correspondence is not as good as for other quantities, fast rotators also preferentially have disky isophotes rather than boxy isophotes (Emsellem et al. 2007).
On the other hand we have the slow rotators, which have complex velocity fields characterized by either an absence of coherent rotation or by multiple kinematic components such as kinematically-decoupled cores. Figure 16.11 demonstrates that slow rotators dominate the population at high stellar mass, \(M_* \gtrsim 2 \times 10^{11}\,M_\odot\), and that they typically display central-density cores. Thus, this all points towards slow rotators being triaxial, because triaxiality is required to explain their complex kinematics and their inner core structure allows for triaxiality to be straightforwardly supported (see Chapter 13.4). However, their observed ellipticity is \(\varepsilon_\mathrm{obs} < 0.4\) and their intrinsic ellipticity is therefore typically small. Taken together with the fact that their orbital anisotropy is similarly small, this indicates that while they are triaxial, they do not strongly deviate from spherical symmetry.
Slow rotators are commonly found in dense environments, such as the centers of groups and clusters, while fast rotators are more generally found in the field like spiral galaxies. Because the slow and fast rotators are distinct in their properties, they likely indicate two different formation mechanisms for elliptical galaxies. The triaxial, cored structure of slow rotators in dense environments is most easily explained as the product of gas-poor major mergers between two galaxies, where the collisionless merger leads to a triaxial final configuration (in much the same way as dark-matter halos in collisionless simulations are triaxial). The orbital structure near the central SMBH provides further evidence for this picture, because the central radial orbits appear to have been scoured by the inspiral of a second SMBH. Fast rotators likely build up much of their mass through gas accretion, much like spiral galaxies, but unlike spirals their star formation is shut off for a variety of reasons (such as the inability to accrete gas after falling into a cluster or group, or feedback from their central SMBH). Growing further through minor mergers, their disks are destroyed and they are puffed up into the observed oblate rotators, but they retain signatures of their origin in the form of disky isophotes and an isotropic orbit distribution around their SMBH. Observations of the age and abundance distribution of elliptical galaxies of different masses and in different environments corroborate this picture (e.g., Thomas et al. 2005; Conroy et al. 2014), with the higher-mass, slow rotators consisting of uniformly old stars enhanced in alpha elements such as oxygen and magnesium, indicative of an early assembly before the gas-poor merger(s) that lead to the final triaxial massive elliptical; while lower-mass, fast rotators have stars with a wider range of ages and the solar-like oxygen/magnesium abundances that result from the more stable star-formation history driven by gas accretion (see the discussion of abundance ratios in Chapter 11.3).
.
.
.