16.2. Schwarzschild modeling and the structure of elliptical galaxies¶
Aside from modeling the dynamics at galaxy centers and aiding in the detection and characterization of SMBHs, one of the other main uses of Schwarzschild modeling has been to study the orbital structure and the mass distribution in the inner regions of elliptical galaxies. As we discussed in Chapter 12.1, the discovery in the late 1970s that massive elliptical galaxies rotate slowly started a rich field of inquiry into the internal dynamics of elliptical galaxies. Between this and the early 2000s, the main progress in studying elliptical galaxies was on the one hand the realization that they must have significantly anisotropic velocity dispersions to satisfy the tensor-virial theorem (see Chapter 14.2), and on the other hand steadily improving observational constraints on their inner structure, isophote shapes, and kinematics. But kinematical studies remained limited to slit-based spectroscopy of one-dimensional slices along the galaxy (e.g., Binney et al. 1990), meaning that a full picture of the kinematics was lacking.
This situation changed with the development of integral-field spectroscopy (IFS), obtaining spectroscopic observations over the two-dimensional face of a galaxy in a single observation to produce a three-dimensional datacube of spectra. One of the first big IFS surveys was the SAURON survey of elliptical and lenticular galaxies (Bacon et al. 2001; de Zeeuw et al. 2002). SAURON selected a representative sample of 48 objects—with galaxies chosen to cover a range of galaxy properties such as luminosity, ellipticity, and environment—to investigate the range of kinematic and stellar-population behavior in elliptical and lenticular galaxies (SAURON also observed 24 Sa galaxies, which we will not discuss here; from now on we will simple say “elliptical” galaxy, but this will typically include the lenticular SAURON galaxies as well, elliptical and lenticular galaxies are in this literature often described as early-type galaxies). The three-dimensional datacubes allow two-dimensional maps of the mean line-of-sight velocity, velocity dispersion, and higher-order moments to be extracted. A first look at the kinematic maps by Emsellem et al. (2004) immediately revealed the large diversity in kinematics among elliptical galaxies. Figure 16.5 shows the mean-velocity maps of 24 galaxies from Emsellem et al. (2007) illustrating the different types of behavior. The black contour is a representative isophote that can be used to gauge whether the kinematic major axis is aligned with the photometric major axis.
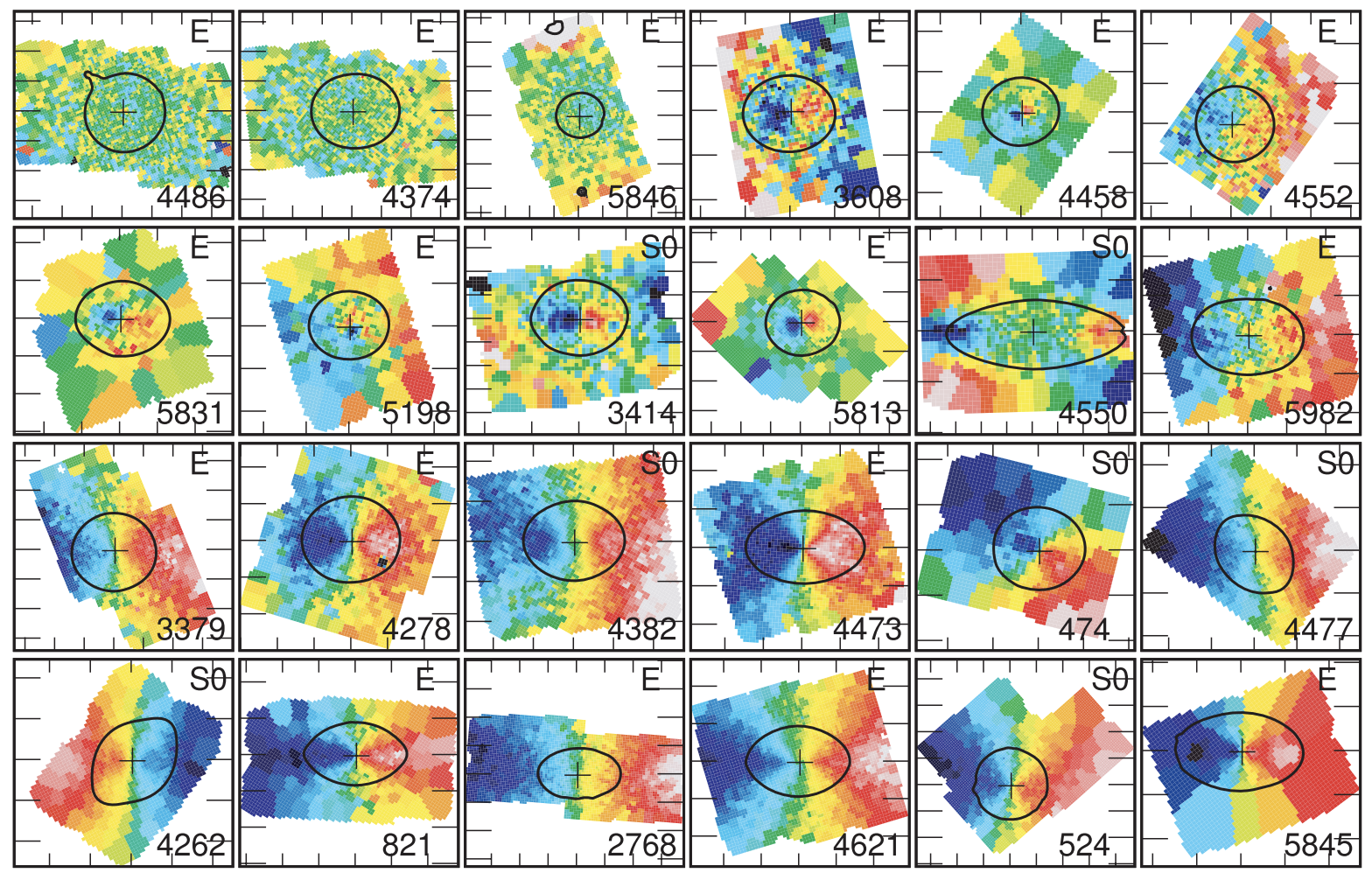
Figure 16.5: Mean line-of-sight velocity maps for 24 elliptical and lenticular galaxies (Emsellem et al. 2007).
The galaxies in this figure are ordered by a measure of how much coherent rotation they show, as the progression towards more and more ordered rotation displays (ordered rotation showing up as the spider-like shape of equivelocity contours, see Chapter 8.1). The remaining 24 galaxies that are not displayed here have similar ordered rotation as the last few in this figure. Thus, it is clear that many elliptical galaxies display ordered rotation aligned with the photometric axes and only a small fraction (about 25% based on Figure 16.5) have velocity fields where the velocity is either entirely disordered or where there are signs of rotation, but they are not coherent throughout the galaxy. Only the first three galaxies display no signs of rotation, while the remaining galaxies in the first two rows either have so-called kinematically-decoupled cores (KDCs; Bender 1988; Jedrzejewski & Schechter 1988), with rotation limited to the very center of the galaxy, counter-rotating disks with rotation opposite to the overall rotation sense of the galaxy (e.g., Rubin et al. 1992; Rix et al. 1992), or a sort of “disordered ordered motion”.
The wealth of data means that we can use Schwarzschild modeling to recover the orbital distribution in great detail. In light of our discussion of the different orbit families in triaxial galaxies in Chapter 13.4, of particular interest is the study of van den Bosch et al. (2008). They implemented a triaxial version of Schwarzschild’s technique (a difficult task as discussed in Chapter 14.3.3) and used it to determine the internal orbital distribution of NGC 4365, an E3 galaxy with a kinematically-decoupled core and a strong misalignment between the kinematic and photometric major axes. The data compared to the best-fit model are shown in Figure 16.6.
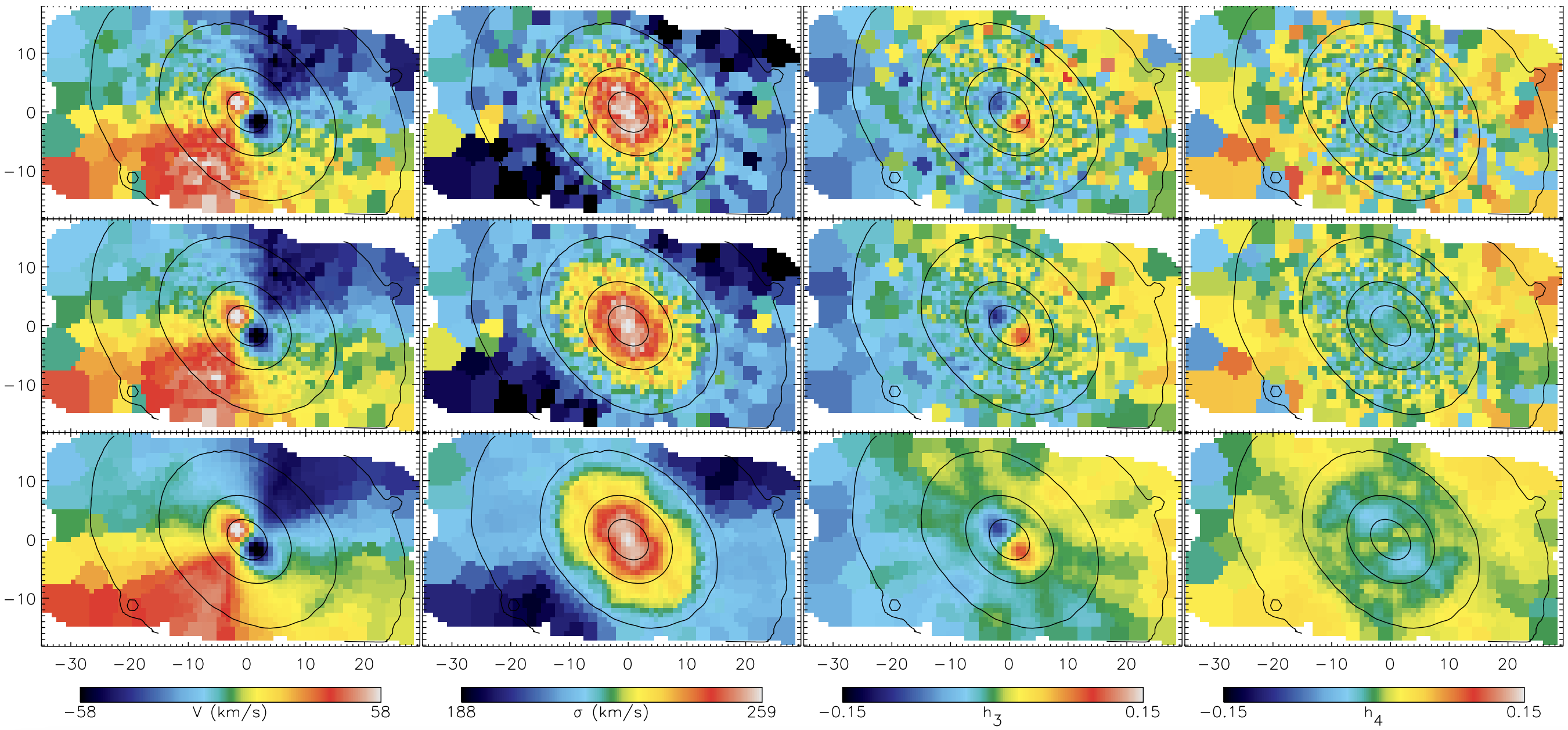
Figure 16.6: Schwarzschild modeling of the massive elliptical NGC 4365 (van den Bosch et al. 2008). The top row has the data, the middle row the data point-symmetrized relative to the center, and the bottom row has the Schwarzschild model.
The data and the model here are represented as the first four moments of the line-of-sight velocity distribution: the mean velocity, velocity dispersion, and the \(h_3\) and \(h_4\) Gauss-Hermite moments (van der Marel & Franx 1993). The kinematics clearly show that NGC 4365 has to be triaxial, because of the minor-axis rotation: the large-scale rotation pattern is aligned with the minor photometric axis (isophotes are shown as contours), rather than with the major axis; only the KDC rotation is aligned with the major photometric axis. The Schwarzschild model provides an excellent fit to the data. We can then use the best-fit Schwarzschild model to look at how the different orbital families contribute to the total density and velocity maps. This is shown in Figure 16.7.

Figure 16.7: Contribution of the different orbit families in triaxial potentials to the mass and kinematics of NGC 4365 (van den Bosch et al. 2008).
The top row displays the combined density, mean velocity, and velocity dispersion from all orbits, while the other rows show the contributions from different orbit families, focusing on the properties of the short-axis tube orbits. The short-axis tube orbits dominate the mass density almost everywhere, but they are made up of a prograde and a retrograde component that are almost equivalent aside from their sense of rotation and, therefore, almost cancel each other’s rotation signal out. Only at the center does this cancellation not happen and the result is the KDC. While the short-axis tubes also give rise to a retrograde overall rotation on larger scales, this is drowned out by the much larger contribution of the long-axis tubes and the resulting rotation pattern on large scales is strongly misaligned with the photometric axes. The orbital structure of NGC 4365 therefore demonstrates how combining the basic orbit families in triaxial potentials can lead to a complex pattern of rotation and velocity dispersion in galaxies.
A closer inspection of the mean-velocity fields from Emsellem et al. (2007) in Figure 16.5 shows that most elliptical galaxies in the SAURON sample do not call for a triaxial analysis, because their kinematics is in most cases aligned with their photometry. For this reason, the SAURON galaxies have not been studied with triaxial modeling, but instead with simple two-integral (Jeans) or three-integral (Schwarzschild) axisymmetric modeling similar to the SMBH analyses discussed in the previous section. Krajnovic et al. (2005) performed a detailed axisymmetric, three-integral Schwarzschild analysis of NGC 2974 and demonstrated that the modeling was able to recover the intrinsic orbital distribution for mock data with similar properties as the best-fit Schwarzschild model to the data. The tests also show that the mass-to-light ratio can be reliably determined using Schwarzschild modeling, but that the inclination is only weakly constrained; the inferred mass-to-light ratio from kinematic data is therefore only weakly dependent on the inclination, a useful property, because it removes the inclination bias that in other situation severely affects inferred properties (such as the intrinsic shape of a galaxy!).
That most SAURON elliptical galaxies can be satisfactorily modeled using three-integral axisymmetric Schwarzschild modeling poses another question: whether they can be modeled using the even simpler two-integral modeling. As we discussed in the previous section, the advantage of two-integral modeling is that the even part of the distribution function \(f(E,L_z)\) is uniquely determined by the density and the odd part by the mean velocity. This means that two-integral models are far easier to implement and fit to data, because we can compute all observable moments of the distribution function using the axisymmetric Jeans equations starting from the (deprojected) density and average rotation velocity \(\overline{v_\phi}(R,z)\), rather than performing computationally-expensive Schwarzschild modeling. The basic answer is that two-integral modeling both does and does not suffice to describe the observed kinematics of elliptical galaxies. It can reliably recover quantities such as the total mass-to-light ratio (Cappellari et al. 2006). But as we saw in Chapter 14.2, elliptical galaxies must deviate from the \(\sigma_z = \sigma_R\) relation inherent in two-integral modeling for their observed shapes to be consistent with their low bulk velocities (this is the case even for most of the elliptical galaxies that display strong rotation). Cappellari et al. (2007) demonstrated this explicitly using three-integral Schwarzschild modeling of a subset of 24 elliptical galaxies in SAURON.
That the mass-to-light ratio can be consistently determined using two- and three-integral Schwarzschild modeling allows one to look for trends in mass-to-light ratio with other galaxy properties. The \(I\)-band mass-to-light ratios \(M/L\) determined by Cappellari et al. (2006) span a range of \(1 \lesssim M/L < 6\) and they are strongly correlated with the luminosity-weighted second moment \(\sigma_e\) of the line-of-sight velocity distribution within the effective radius as \begin{equation}\label{eq-massellip-ML-funcof-sigma} {M\over L} = 3.80\,\left({\sigma_e \over 200\,\mathrm{km\,s}^{-1}}\right)^{0.84}\,, \end{equation} with a scatter of only \(\approx 0.2\,\mathrm{dex}\) in \(\log_{10} M/L\) at a given \(\sigma_e\). This is a similar relation as the M-sigma relation for SMBHs and their host velocity dispersion. The variation in the mass-to-light ratio inferred from the dynamical analysis is partly due to changes in the dark-matter contribution within the effective radius, which is higher for more massive galaxies. But the main reason for the difference in \(M/L\) is a changing stellar population with galaxy mass, with more massive galaxies having older populations with higher \(M/L\) than less massive galaxies. The tight relation between \(M/L\) and \(\sigma_e\) furthermore has implications for the most important scaling relation for elliptical galaxies, the fundamental plane, which we discuss in more detail in Chapter 18.4. The fundamental plane is a tight relation between the effective radius, velocity dispersion, and the surface brightness at the effective radius (Djorgovski & Davis 1987; Dressler et al. 1987). Under the assumption of constant \(M/L\) and orbital structure, the fundamental plane can be derived using the virial theorem (see Equation 18.37 later), but there is an offset between the virial-theorem prediction and the actually observed relation, known as the tilt of the fundamental plane. The \(M/L-\sigma_e\) relation can explain 90% of this tilt, demonstrating that the tilt is mainly due to differences in \(M/L\) rather than significant differences in the orbital structure among elliptical galaxies.
The SAURON survey thus demonstrated that elliptical galaxies display an interesting variety in observed kinematics, including completely disordered motion, various degrees of more ordered kinematics, and clean rotational systems. SAURON further showed that quantities derived from the two-dimensional kinematic maps such as the orbital anisotropy and the mass-to-light ratio contain important information about the formation and evolution of elliptical galaxies. As is often the case, the way forward was to go from the representative SAURON sample to statistical samples that are selected in a well-defined manner from the parent galaxy population and that therefore can be related back to the full population. However, the SAURON analyses also showed that two-integral modeling does not suffice to fully describe the observed kinematics, yet Schwarzschild modeling is computationally-expensive and labor-intensive and therefore difficult to apply to the much larger statistical samples. However, it turns out that there is a simple way to generalize the two-integral method to an effective three-integral method that retains the simplicity of the two-integral modeling, but also attains the realism of the three-integral Schwarzschild modeling. We discuss this in the next section.

