6.7. Ultra-diffuse galaxies and Dragonfly 44¶
We can use the Wolf estimator to learn about the nature of a population of galaxies that has recently garnered much interest: ultra-diffuse galaxies (UDGs). These are galaxies that have a very low surface brightness and low luminosity, comparable to that of the dwarf spheroidals that we discussed earlier in this chapter, but that have sizes that are an order of magnitude larger, making them of similar size to large galaxies like the Milky Way, even though they contain orders of magnitude fewer stars. These galaxies have primarily been found in galaxy clusters, such as the Coma cluster (van Dokkum et al. 2015a; Koda et al. 2015). We discuss UDGs and other galaxy types in more detail in Chapter 18.3.
How these UDGs form is a bit of a mystery and one important ingredient in the puzzle is what their total masses are (stars, gas, and dark matter). This can shed light on the type of potential well that the stars in these galaxies formed in and can help understand how these galaxies are able to survive in a cluster environment, where small galaxies are likely to be tidally pulled apart. Because of their low surface brightness, obtaining velocity dispersions for these systems is difficult, but a few groups have done so and we can interpret these measurements using the Wolf estimator to determine the total mass of some of the UDGs. Before embarking on this, we should note that the Wolf estimator (and all of the mass modeling approaches that we have discussed so far) assume dynamical equilibrium for the tracer stars, which may not be a good assumption if the UDGs are strongly tidally interacting with their host clusters. But we will boldly move ahead under the assumption of dynamical equilibrium and see whether a consistent picture emerges.
A first measurement of the velocity dispersion of a set of tracers in a UDG was presented by Beasley et al. (2016). Figure 6.5 displays an image of the ultra-diffuse galaxy VCC 1287 in the Virgo cluster:
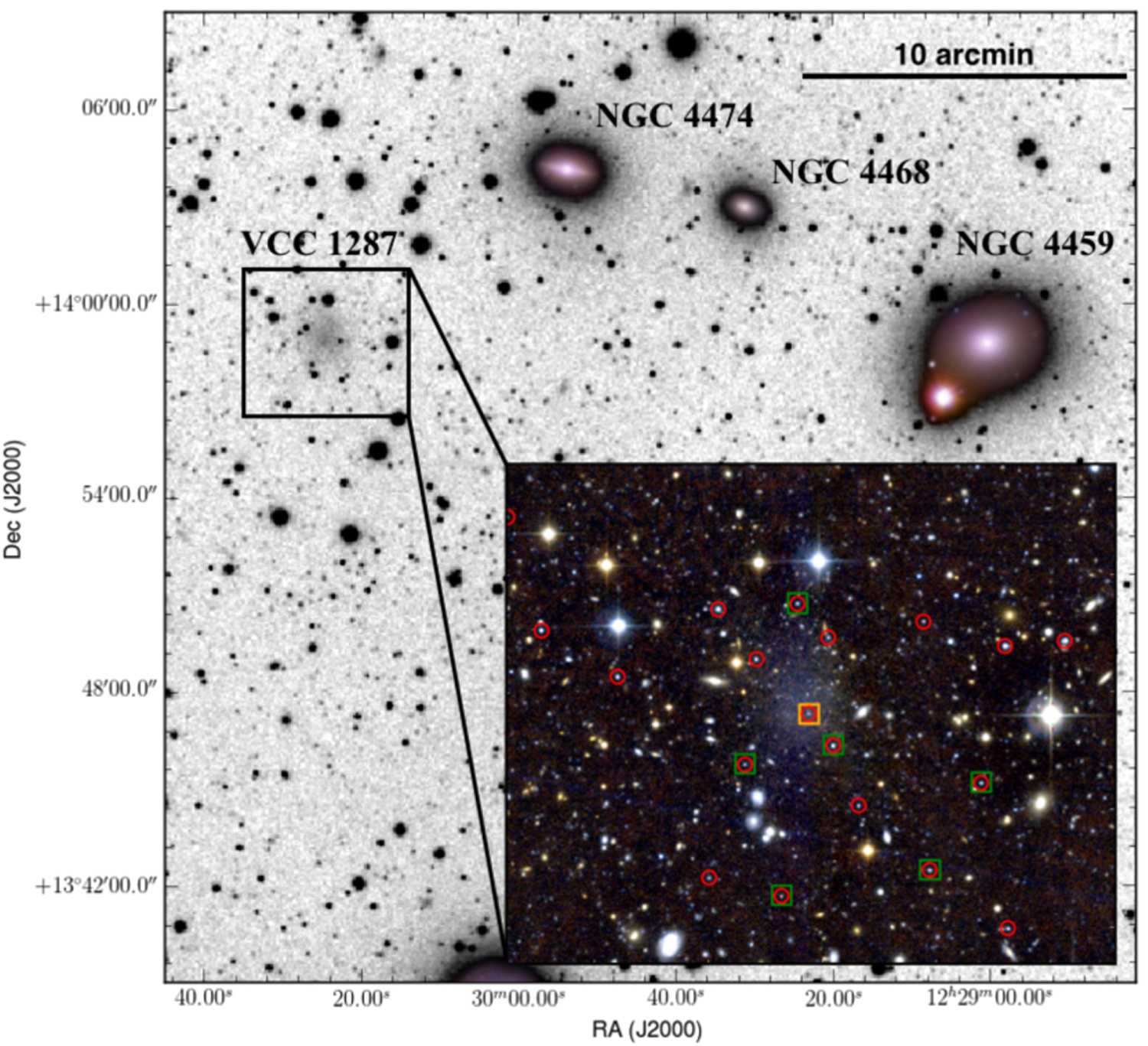
Figure 6.5: The ultra-diffuse galaxy VCC 1287 (Beasley et al. 2016).
The authors of this work identified candidate globular clusters associated with VCC 1287 and measured their line-of-sight velocities. They found seven globular clusters that are likely associated with VCC 1287, which are indicated by the green and orange boxes in Figure 6.5. For these clusters, they measure a line-of-sight velocity dispersion of \(\sigma_\mathrm{los} = 33^{+16}_{-10}\,\mathrm{km\,s}^{-1}\). The half-mass radius of this system is approximately \(R_e \approx 2.4\,\mathrm{kpc}\), and using the Wolf estimator from Equation (6.29) gives a mass within the half-light radius of \(2.4^{+2.9}_{-1.3}\times 10^9\,M_\odot\):
[9]:
# Function that gives Wolf estimate
import astropy.constants as apyconst
def wolf_estimator_re(sig_los,Re):
return (4.*sig_los**2.*Re/apyconst.G).to(10**9*u.Msun)
# Apply to VCC 1287
sig_los= 33.*u.km/u.s
sig_los_up= 49.*u.km/u.s
sig_los_down= 23.*u.km/u.s
Re= 2.4*u.kpc
print(f"""The mass of VCC 1287 from the Wolf estimator is {wolf_estimator_re(sig_los,Re):.2f}
with uncertainty +{(wolf_estimator_re(sig_los_up,Re)
-wolf_estimator_re(sig_los,Re)):.2f} and -{(wolf_estimator_re(sig_los,Re)
-wolf_estimator_re(sig_los_down,Re)):.2f}""")
The mass of VCC 1287 from the Wolf estimator is 2.43 1e+09 solMass
with uncertainty +2.93 1e+09 solMass and -1.25 1e+09 solMass
Combined with the total stellar luminosity, this gives a mass-to-light ratio \(M/L \approx 100\) within \(R_e = 2.4\,\mathrm{kpc}\). The half-mass radius is close to the center and if these UDGs are embedded in dark-matter halos—as certainly seems to be the case from the large \(M/L\)—then these halos extend to much larger radii. By extrapolating the enclosed mass at \(1\,R_e\) to an estimate of the total halo mass, Beasley et al. (2016) find a total dark-matter mass of \(\approx 10^{11}\,M_\odot\). This makes VCC 1287 a very large galaxy indeed. But the uncertainty in the mass is quite large, because of the large uncertainty in \(\sigma_\mathrm{los}\).
Dragonfly 44 is another ultra-diffuse galaxy for which the line-of-sight velocity dispersion was measured. van Dokkum et al. (2016) obtained deep Keck spectroscopy of Dragonfly 44 to measure the stellar velocity dispersion. Dragonfly 44 is a UDG in the Coma cluster and is shown in Figure 6.6.

Figure 6.6: Dragonfly 44 (van Dokkum et al. 2016).
They obtained a velocity dispersion of \(\sigma_\mathrm{los} = 47^{+8}_{-6}\,\mathrm{km\,s}^{-1}\), with no evidence of a radial trend in \(\sigma_\mathrm{los}\). This velocity dispersion was later revised down to \(\sigma_\mathrm{los} = 33\pm3\,\mathrm{km\,s}^{-1}\) based on further, spatially-resolved measurements of the dipsersion profile (van Dokkum et al. 2019). The assumptions underlying the Wolf estimator are therefore satisfied and we can combined \(\sigma_\mathrm{los}\) with the measured half-mass radius \(R_e = 3.5\,\mathrm{kpc}\) to give a mass within the half-light radius of \(3.5^{+0.7}_{-0.6}\times 10^9\,M_\odot\):
[10]:
# Apply to Dragonfly 44
sig_los= 33.*u.km/u.s
sig_los_up= 36.*u.km/u.s
sig_los_down= 30*u.km/u.s
Re= 3.5*u.kpc
print(f"""The mass of Dragonfly 44 from the Wolf estimator is {wolf_estimator_re(sig_los,Re):.2f}
with uncertainty +{(wolf_estimator_re(sig_los_up,Re)
-wolf_estimator_re(sig_los,Re)):.2f} and -{(wolf_estimator_re(sig_los,Re)
-wolf_estimator_re(sig_los_down,Re)):.2f}""")
The mass of Dragonfly 44 from the Wolf estimator is 3.54 1e+09 solMass
with uncertainty +0.67 1e+09 solMass and -0.62 1e+09 solMass
The mass-to-light ratio within the half-mass radius is \(M/L \approx 25\), corresponding to a dark matter fraction of \(\approx 95\,\%\) within \(r_{1/2} \approx 1.33\,R_e = 4.6\,\mathrm{kpc}\). Extrapolating the mass to the total mass of the dark-matter halo gives a mass of \(\approx 10^{11}\,M_\odot\), similar to VCC 1287 above. This demonstrates that relatively-massive galaxies with mass-to-light ratios characteristic of dwarf spheroidal galaxies are quite common in the Universe. This is surprising, because most relatively-massive galaxies have much lower mass-to-light ratios. For example, the Milky Way, which is only an order of magnitude more massive in total dark matter, has a dark-matter fraction at \(r\approx 3.5\,\mathrm{kpc}\) of only \(\approx30\,\%\) and the mass is dominated by stars (see Figure 1.14).

