6.5. The masses of dwarf spheroidal galaxies using the Jeans equation¶
Dwarf spheroidal galaxies (dSphs) are low-luminosity, low-mass galaxies that are the smallest galaxies that form in the Universe. Galaxy formation and evolution in such galaxies is very different from that in large galaxies like the Milky Way. dSphs therefore present a unique laboratory for finding the threshold of galaxy formation: how do stars form in low-mass galaxies, how do they enrich their interstellar medium, what happens to these galaxies as they accrete onto larger galaxies, and, importantly, what are their dark-matter distributions? We focus on the latter question here and discuss dSphs and other galaxy types in more detail in Chapter 18.3.
dSphs are commonly found around the Milky Way, where we can see the lowest luminosity galaxies that are too dim and too low in surface brightness to be seen around external galaxies. Determining the masses and mass-to-light ratios of these galaxies is important for different reasons: (i) the ratio of stellar-to-dark-halo mass in these galaxies tells us about the efficiency of star formation in low-mass galaxies, (ii) because the mass-to-light ratios of these galaxies appear to be high they are dominated by dark matter at all radii and can therefore provide a clean look at the dark-matter distribution in galaxies (although whether this is really true is still under debate), and (iii) if dark matter would happen to annihilate, these galaxies make for good targets to see the products of such annihilation (e.g., Springel et al. 2008b).
Around the Milky Way, we have so-called classical dwarfs spheroidals like Draco, Fornax, and Sculptor and ultra-faint dwarf spheroidals. The former have been known for decades and they are relatively massive with stellar masses of about \(10^6\) to \(10^7\,M_\odot\). The latter have very low surface brightness and low stellar masses; they were only discovered using wide-field multi-band surveys like SDSS (e.g., Willman et al. 2005, Belokurov et al. 2007) and DES (e.g., Bechtol et al. 2015) that allow slight stellar overdensities in the stellar halo to be detected. For the classical dSphs, large spectroscopic data sets of line-of-sight velocities have been obtained, for example, the data set from Walker et al. (2009a), represented Figure 6.2.
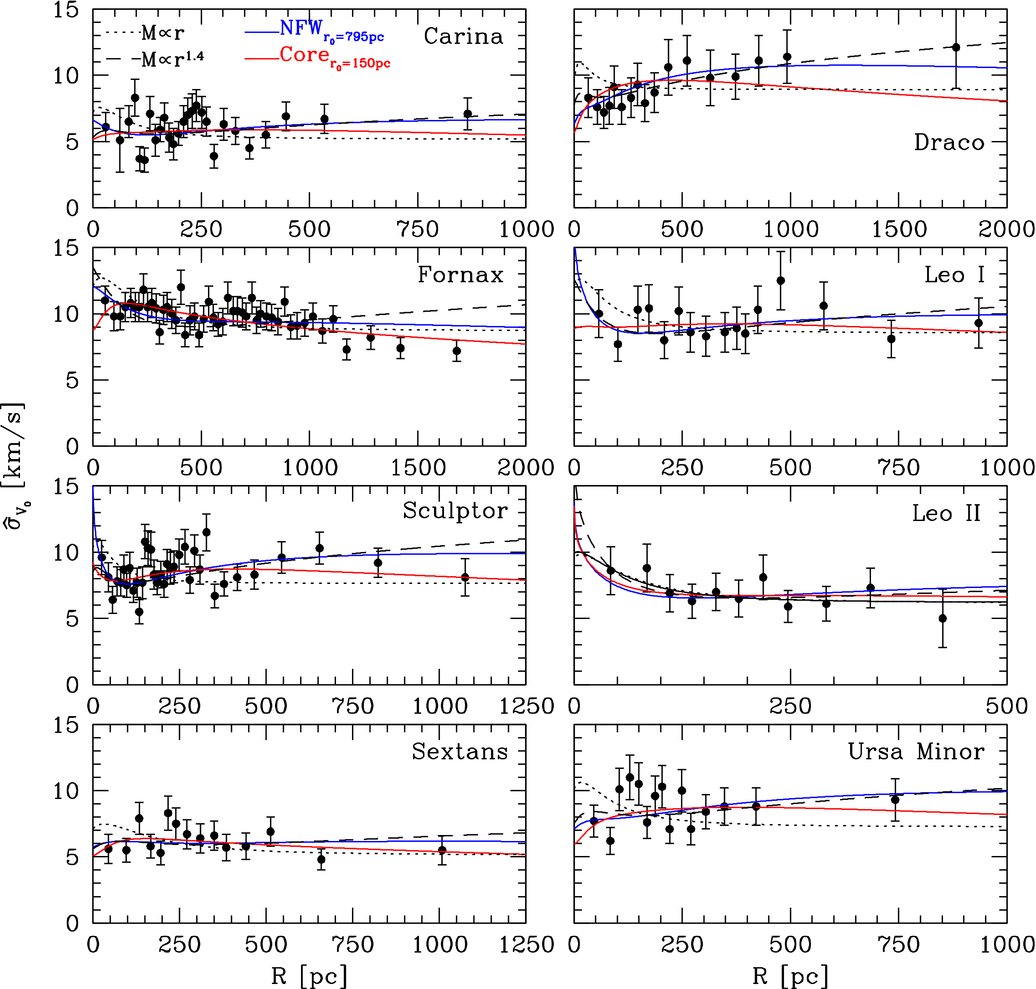
Figure 6.2: Velocity dispersion profiles for classical dSphs in the Milky Way from Walker et al. (2009b).
These data can be used to measure the masses and mass profiles of dSphs using dynamical modeling. Measurements of the surface-density profile \(\Sigma(R)\) are available for these dSphs from direct star counts. These can be deprojected to three-dimensional density profiles \(\nu(r)\) for use in, e.g., the Jeans equation. One way of doing this is by fitting the surface-density profile with a simple form, such as a Plummer profile (see Chapter 2.4.3) , which provides a good fit to the observed surface-density profiles of dSphs. The two-dimensional projection of the Plummer profile is \begin{equation} \Sigma(R) = \frac{M_*}{\pi\,R_e^2}\,\frac{1}{\left(1+R^2/R_e^2\right)^2}\,, \end{equation} for a total stellar mass \(M_*\) and a two-dimensional half-mass radius \(R_e\) (that is, the cylindrical radius that contains half of the stellar mass). Once the surface-density profile has been fit with a Plummer profile, the three-dimensional density of this profile can be used. Another option is to use the fact that if we assume that the underlying profile is spherically symmetric, the surface density \(\Sigma(R)\) is related to the three-dimensional density \(\nu(r)\) as follows \begin{align} \Sigma(R) & = 2\,\int_0^\infty \mathrm{d} z \,\nu(\sqrt{R^2+z^2})= \int_R^\infty \mathrm{d} r^2 \,\nu(r)\,\frac{1}{\sqrt{r^2-R^2}}\,. \end{align} This is an Abel integral equation, which can be inverted to (see Appendix B.4.1) \begin{equation}\label{eq-3ddens-2ddens} \nu(r) = -\frac{1}{\pi}\,\int_r^\infty\mathrm{d}R\,\frac{\mathrm{d} \Sigma(R)}{\mathrm{d} R}\,\frac{1}{\sqrt{R^2-r^2}}\,. \end{equation} Thus, we can directly recover the three-dimensional density \(\nu(r)\) from a measurement of the projected surface density \(\Sigma(R)\).
The second ingredient for the spherical Jeans equation is \(\sigma^2_r(r)\). However, the measurements of the line-of-sight velocities in dSphs give \(\sigma_\mathrm{los}^2\). While in the Milky Way analysis above \(\sigma_r \approx \sigma_\mathrm{los}\), this is only due to our position close to the center of the Milky Way. For external systems, we cannot set \(\sigma_r = \sigma_\mathrm{los}\). Instead, we need to compute \(\sigma_\mathrm{los}(R)\) from \([\Sigma(R),\nu(r),\sigma_r(r),\beta]\). Binney & Mamon (1982) demonstrated that \(\sigma_\mathrm{los}(R)\) is given by \begin{equation}\label{eq-surfdens-siglos-jeans} \Sigma(R)\,\sigma_\mathrm{los}^2(R) = 2\,\int_R^\infty\,\mathrm{d}r\,\left(1-\beta(r)\,\frac{R^2}{r^2}\right)\,\frac{\nu(r)\,\sigma_r^2\,r}{\sqrt{r^2-R^2}}\,. \end{equation} Assuming some form of \(\beta(r)\), we can substitute \(\nu(r)\,\sigma_r^2\) obtained from the integrated Jeans equation (equation 5.49 for constant \(\beta\) or equation 5.51 for general \(\beta(r)\) profiles) in this equation and predict \(\sigma_\mathrm{los}\) for a given \([\nu(r),\Sigma(R)]\) pair (related through Equation 6.17), an assumed mass profile \(M(<r)\), and the anisotropy \(\beta(r)\). This predicted \(\sigma_\mathrm{los}\) can then be compared to the data and the (parameters of) the mass profile \(M(<r)\) can be adjusted to give the best fit.
This type of analysis was performed by, e.g., Walker et al. (2009b) using the \(\sigma_\mathrm{los}\) data above to determine the mass profiles of 8 classical dwarf spheroidals. They found that they were in particular able to robustly determine the mass within \(R_e\) (which they denote as \(r_\mathrm{half}\)), largely independent of the value of \(\beta\). The measured \(M(<R_e)\) and average densities within \(R_e\) are displayed in Figure 6.3.
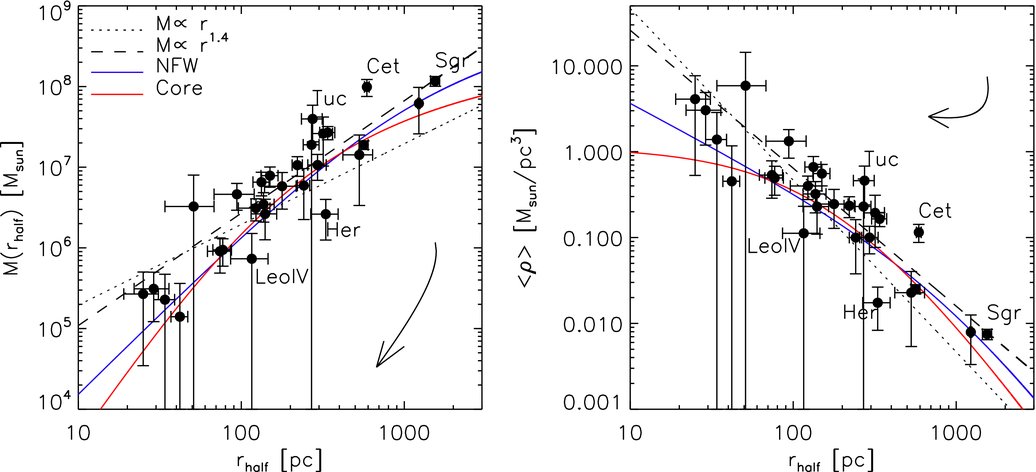
Figure 6.3: Mass-profile properties of Milky-Way classical dSphs from Walker et al. (2009b).
These results imply that the dSphs are embedded in massive dark-matter halos, with mass-to-light ratios of 10 to 100. The Jeans analysis of these data, however, is not sensitive to the inner profile of the dark-matter halo and in particular cannot easily distinguish between a cored (\(\rho \propto\mathrm{constant}\)) or a cuspy (\(\rho \propto r^{-1}\)) profile. This is an important question, as the prediction from the reigning cold dark-matter paradigm is that the inner profiles should be cuspy (although the exact prediction depends on uncertain baryonic feedback effects).

