11.1. Chemical enrichment processes in galaxies¶
On a basic level, galaxies consist of dark matter, stars, and gas. After the formation of the dark-matter halo (discussed in more detail in Chapter 17), dark matter plays a largely passive role as the gravitational stage upon which stars and gas perform an elaborate dance. Stars in the Universe by and large form in the disks of large galaxies like the Milky Way, from cold gas that forms a thin layer embedded within the thicker galactic disk (the interstellar medium; ISM). When stars form from gas that has cooled to form molecular clouds, they inherit the abundances of the ISM at the time of their formation. As stars age and massive stars die, some or all of their material is returned to the ISM as ejecta, (partially) enriched through nucleosynthesis during a star’s regular life and (sometimes) violent, explosive death. This ‘enriches’ the ISM, that is, it increases the fractional abundance of heavy elements in the ISM. Inflows of gas from the intergalactic medium (IGM) and outflows driven into the IGM by, e.g., supernova explosions, further affect the abundance of heavy elements in the ISM at any given time, typically lowering it. But overall, the evolution is such that the enrichment of the ISM by stellar nucleosynthesis leads to a steady increase in the abundance of heavy elements in the ISM over time.
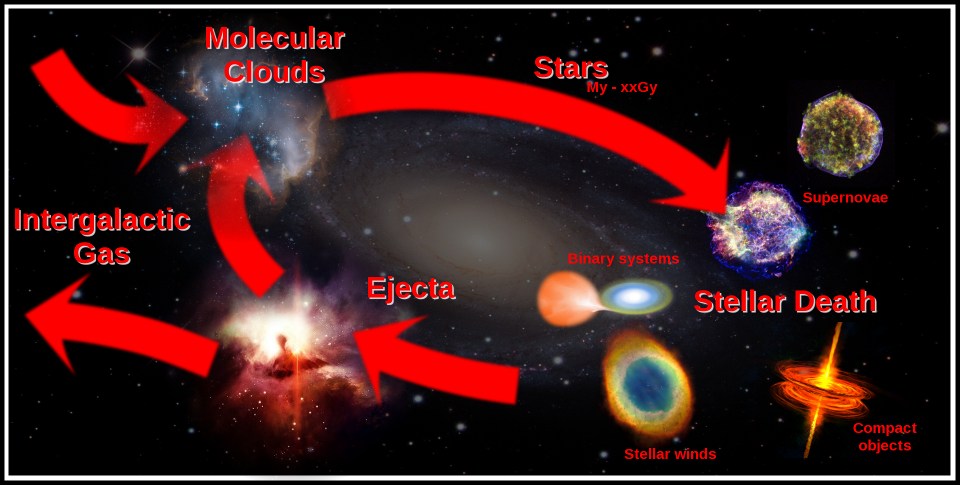
Figure 11.1: The baryon cycle in galaxies (credit: Richard Longland).
This cycle is shown in Figure 11.1.
The previous paragraph presents an overly simplified picture, but is nevertheless a useful starting point to consider the chemical evolution of galaxies. In detail, the dark matter distribution may evolve during the evolution of galaxies and it may itself be affected by the outflows driven by supernovae and other feedback processes (see Chapter 19.3.3). Star-forming gas is observed to form a thin layer in present-day galaxies, but may not have been as thin earlier in the evolution of the Universe. Infalling gas from the IGM typically has a lower heavy-element abundance than the ISM, but galactic fountains (where gas driven out of one part of the galaxy by outflows returns to a different part of the galaxy) can lead to inflows with higher abundances. For some changes in the rate of star formation and the rate at which gas is lost to outflows, the heavy-element abundance of the ISM can even decline in time. And as the previous chapters have made clear, stars are not static, but orbit within the galaxy over their lifetimes. Thus, enriched ejecta may be returned at very different locations from where a star was born.
Observational galactic astronomy is limited to observing the properties of celestial objects at a single moment. For the Milky Way, this is the present (the light travel time from the furthest reaches of the Galactic halo is \(\lesssim 100,000\) years, much smaller than the shortest time scale over which galactic evolution operates). We can therefore only directly determine the heavy-metal abundance of the ISM in the Milky Way as it is today (and even this is difficult). External galaxies observed at moderate or high redshift can give a direct view of the ISM abundance at earlier times, but again only at a single time for a given galaxy. We cannot for a single galaxy directly determine how the ISM abundance changes over time. However, while nuclear burning changes the elemental abundances in the inner parts of a star, the abundances of elements in the stellar photosphere near the surface remain by and large unchanged over the lifetime of a star. Because the photospheric abundances are those that are most easily determined, using spectroscopic observations, the observed heavy-metal abundances of stars today therefore measures the abundances of the ISM when the star was formed. Thus, the elemental abundances of a sample of stars formed over the lifetime of a galaxy allows us to indirectly constrain the chemical evolution of the ISM. Such elemental abundances of a sample of stars can be obtained by measuring abundances for individual stars in the Milky Way through, typically, high-resolution spectroscopy or using stellar-population-synthesis modeling of the integrated spectrum of an external galaxy (see Chapter 18.1).
As an example of a measurement of the abundances of different elements, we can look at the abundances of the Sun as determined by high-resolution spectroscopy of the solar photosphere by Asplund et al. (2009), shown in Figure 11.2.
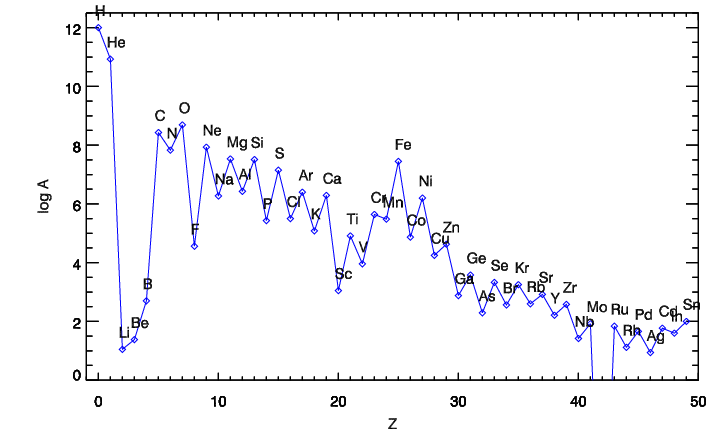
Figure 11.2: The abundances of different elements in the Sun (Bergemann & Serenelli 2014).
The abundances by number of atoms of different elements are displayed on a logarithmic scale where the number of hydrogen atoms in the Sun is defined to be \(10^{12}\). To obtain the abundances by mass one would have to multiply by the atomic weight of each element (see Equation 11.48 below). It is clear that the pattern of abundances is complex, with an overall decline towards higher \(Z\), an alternating even/odd-\(Z\) pattern, a severe dip for the light elements lithium (Li), beryllium (Be), and boron (B) and a peak around iron (Fe). These trends reflect the relative ease with which these elements are created and destroyed in the Universe (Burbidge et al. 1957). The lightest elements in the Universe, He and Li, were created in the early Universe in a process called Big Bang nucleosynthesis. All elements heavier than boron that naturally occur in the Universe are believed to form in stars or stellar explosions, including some of the most extreme and energetic processes in the evolution of stars (beryllium and boron form primarily by the breaking up of heavier elements in the ISM when they collide with cosmic rays, a process called cosmic ray spallation). The processes that create carbon, nitrogen, oxygen, and heavier elements fall in four broad classes:
Type II supernovae (type II SNe): massive stars (\(M \gtrsim 8\,M_\odot\)) explode as core-collapse supernovae when nuclear burning in the star has reached its endpoint through the formation of an iron/nickel core that cannot uphold the gravity of the star. The ensuing explosion returns material enriched through quiescent stellar nucleosynthesis before the explosion (producing most of the abundance of even-\(Z\) elements lighter than silicon) as well material enriched through explosive nucleosynthesis during the explosion (producing odd-\(Z\) elements and even-\(Z\) elements starting with silicon). Type II supernovae enrichment is responsible for much of the abundance of elements between carbon and scandium and some of the abundance of elements from titanium to zinc (Andrews et al. 2017). Elements whose most abundant isotope are integer multiples of the Helium nucleus (C, O, Ne, Mg, Si, S, Ar, Ca, and Ti; collectively known as alpha elements) are especially efficiently produced through the alpha process. Many of these are easy to observe, and while the contribution of Type II supernovae enrichment to their observed abundance varies (roughly decreasing with atomic mass starting at O and excluding C, which is primarily produced through the s process discussed below), they are often used to trace Type II supernovae enrichment. Overall, about 90% of all of metals in the Universe are produced by type II supernovae.
Type Ia supernovae (type Ia SNe): low-mass stars end their lives as white dwarfs, which are normally stable. But they can become unstable if they accrete mass from a giant companion (now considered to not significantly contribute to the number of type Ia SNe) or when they slowly (through binary inspiraling) or quickly (through direct collisions) merge with another white dwarf, at which point they explode. Heavy metals returned to the ISM by type Ia supernovae are almost all formed in the explosive nucleosynthesis stage, producing elements from silicon to zinc like for type II SNe. The combination of type II and type Ia SNe enrichment accounts for about 99% of all of the metals in the present-day Universe and for all of the abundances of elements from oxygen to zinc.
The s process: Elements heavier than zinc are believed to be produced through neutron-capture processes, where repeated cycles of neutron capture(s) and beta decay allow elements with higher and higher numbers of nucleons to be formed. The way in which this process occurs is classified into two classes depending on whether the neutron captures occur slowly (for the s [slow] process) or rapidly (for the r [rapid] process) compared to the typical time scale for beta decay of the element in question (which can be minutes to thousands of years or more depending on the isotope in question). Both of these broad processes have multiple basic mechanisms contributing them, with the s process occurring during helium-shell burning in asymptotic giant branch (AGB) stars as well as during helium burning in the cores of very massive stars; both of these occurring on time scales of hundreds of thousands of years. The products from s-process enrichment are ejected into the ISM through stellar winds or during the final demise of the star. Besides creating about half of the abundance of elements heavier than zinc, s-process enrichment is also a major contributor to the abundance of carbon and nitrogen in the Universe.
The r process: Like the s process, the r process creates elements heavier than iron, but in environments where neutron captures occur on much shorter time scales than that of the relevant beta decay. Such environments must be neutron rich and the sites of the r process still remain somewhat mysterious. Neutron-star mergers were long suspected of playing a role in the r process and this role was confirmed during the first observed neutron-star merger, known as GW170817, whose light-curve indicated the presence of ejecta rich in elements produced by the r process (Drout et al. 2017; Kasen et al. 2017). However, it remains unclear what the other sites of the r process are, because the observed chemical evolution of r-process elements indicates that a mechanism that returns r-process enriched ejecta quickly after star formation must be present, while neutron-star mergers typically occur only billions of years after star formation. Like the s process, r-process enrichment creates about half of the abundance of elements heavier than zinc.
The relative contribution to the abundance of elements from these four classes (six when including Big Bang nucleosynthesis and cosmic ray spallation) for a star like the Sun is summarized in the chart shown in Figure 11.3.
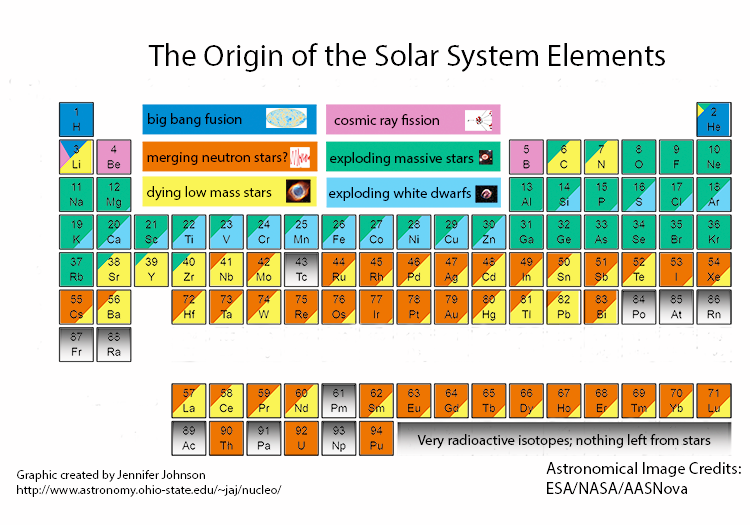
Figure 11.3: Origin processes for elements in the Sun (credit: Jennifer Johnson; CC-BY-SA; Johnson 2019; Johnson et al. 2020).
The four classes discussed above each enrich the ISM on different typical times after star formation creates a new population of stars. Some, especially the r process, may consist of sub-classes that have themselves different typical times. Because enrichment due to type II supernovae happens at the end of massive stars’ lives, the time scale is that of the lifetime of high-mass stars, which is about 5 to 40 Myr for the relevant stars (\(8 \lesssim M/M_\odot \lesssim 50\)); this is short compared to other time scales relevant to galactic evolution. Type Ia supernovae occur when a white dwarf formed at the end of a low-mass star’s life explodes and therefore requires at least the lifetime of the most massive stars that form white dwarfs (tens of millions of years) to start occurring. All proposed mechanisms for how stable white dwarfs turn unstable have a typical time scale of a billion year, so type Ia enrichment occurs on Gyr time scales (but with a significant prompt [\(< 0.5\) Gyr] contribution and a wide distribution of possible times; see Section 11.3.1 below). The main contribution to the s process comes from AGB stars, a late stage in the stellar evolution of \(M \lesssim 8\,M_\odot\) stars that typically lasts about 1 Myr, but only occurs near the end of a star’s life and AGB s-process enrichment therefore occurs on the wide range of time scales corresponding to the lifetimes of low- and intermediate-mass stars. As discussed already above, r-process enrichment from neutron-star mergers has a typical time scale of Gyr because of the long time required for neutron stars to spiral in towards a merger. But r-process enrichment due to, e.g., collapsing, rotating massive stars would occur on the same few Myr time scale as type II supernovae (Siegel et al. 2019). Because of these different time scales, the picture presented above on the relative contribution from the different classes to the abundance of different elements changes when we look at stars formed at different times, like early after the formation of a galaxy.
The amount of a particular element returned to the ISM by the various enrichment processes is called the yield, defined as the amount of mass of element X per solar mass of stars formed. These yields depend on the mass of the star, its own elemental abundance mix, and possibly on properties such as the initial rotation, mass transfers from binary companions, etc. Yields are calculated using stellar models including all known nucleosynthetic pathways. For example, a core-collapse supernova of a \(35\,M_\odot\) star produces \(\approx5\,M_\odot\) of oxygen and \(\approx1\,M_\odot\) of carbon (Chieffi & Limongi 2004). For studying galactic chemical evolution, what we care about is not the yield of each individual star, but the yield from an entire population of stars formed at the same time (a star-formation event) at a given time after time star formation. To obtain these population yields, we need to integrate the individual-star yields over the distribution of stellar masses (the initial mass function of stars, IMF; see Chapter 18.1.3). As an example, integrating over an entire stellar population, we have that a core-collapse supernova creates \(\approx0.016\,M_\odot\) of oxygen per solar mass of stars formed. This number is much smaller than the yield of an individual high-mass star, because it takes into account the large amount of mass in low-mass stars that do not explode as core-collapse supernovae and therefore return zero oxygen via this process. Population-level yields in detail depend on the ISM abundance of the stellar population at formation. Because the IMF necessary to integrate the individual-star yields into population yields could plausibly change with time and/or environment, yields could also depend on the time at which stars form. Assuming that the IMF is constant in time, the total yield of all metals is \(\approx 0.035\,M_\odot\) for every solar mass of stars formed at solar metallicity, with \(\approx 90\%\) of this contributed by type II supernovae, \(\approx 8\%\) by type Ia supernovae, and \(\approx 1.5\%\) from AGB winds. The total yield declines towards lower metallicity because of declining core-collapse yields, settling at \(\approx 0.025\,M_\odot\) at \(Z \lesssim Z_\odot/10\).
The aim of this chapter is to obtain a basic understanding of galactic chemical evolution through simple models that capture much, but not all, of the relevant physics and to use this to comprehend the present-day distribution of metals and the observed ratios of abundances of different elements in a disk galaxy like the Milky Way.

