10.4. The vertical equilibrium state of disks¶
We now turn to a discussion of the vertical equilibrium of galactic disks. Like for the equilibrium states in the disk’s mid-plane, we will learn many useful things about the vertical equilibrium by working in the approximation that the vertical motion is decoupled from the planar motion in galactic disks, which is a good assumption for orbits that do not venture too far from the mid-plane (Chapter 9.2). For the vertical motion this leads to an especially simple system: the system is one-dimensional, with a two-dimensional phase-space \((q,p) = (z,v_z)\), and the vertical specific energy \(E_z = v_z^2/2 + \Phi_z(z)\) is an integral of the motion. The equilibrium collisionless Boltzmann equation for this one-dimensional system is \begin{equation} \dot{q}\,\,\frac{\partial f}{\partial q} + \dot{p}\,\frac{\partial f}{\partial p} = 0\,, \end{equation} or in Cartesian coordinates \begin{equation}\label{eq-equil-boltzmann-1d} v_z\,\,\frac{\partial f}{\partial z} -\frac{\mathrm{d} \Phi_z(z)}{\mathrm{d}z}\,\,\frac{\partial f}{\partial v_z} = 0\,. \end{equation} Because the vertical energy is an integral of the motion, any function that only depends on the phase-space coordinates through the energy, \(f(z,v_z) \equiv f(E_z[z,v_z])\), is a solution of the equilibrium collisionless Boltzmann equation. Conversely, because phase-space is only two-dimensional, any equilibrium solution only depends on the phase-space coordinates through the vertical energy. Therefore, we only need to consider functions of the vertical energy to study equilibrium solutions (of course, we can consider other integrals as well, but these are all functions of the vertical energy).
As we already discussed in Chapter 9.3.1, the Poisson equation takes on an approximate special form in galactic disks. Therefore, the vertical dynamics of galactic disks is approximately a truly one-dimensional dynamical system. The Poisson equation in cylindrical coordinates is \begin{align} 4\pi\,G\,\rho & = \frac{1}{R}\,\frac{\partial}{\partial R}\left(R\,\frac{\partial \Phi}{\partial R}\right) + \frac{\partial^2 \Phi}{\partial z^2}\approx \frac{1}{R}\,\frac{\mathrm{d} v_c^2}{\mathrm{d} R} + \frac{\partial^2 \Phi}{\partial z^2}\,.\label{eq-poisson-vertical} \end{align} In many galactic disks, \(\frac{\mathrm{d} v_c^2}{\mathrm{d} R} \approx 0\), because their rotation curves are close to flat. But more generally, at a given \(R\), the first term on the right-hand side in Equation (10.35) is very close to a constant up to multiple kpc for galactic mass distribution, even when it is non-zero (this was demonstrated using very general arguments by Bovy & Tremaine 2012). Thus, the first term gives rise to a small “phantom density” \(4\pi\,G\,\rho_\mathrm{RC}(R) = \frac{1}{R}\,\frac{\mathrm{d} v_c^2}{\mathrm{d} R}\) and we obtain a one-dimensional version (that is, at a constant radius) of the Poisson equation in galactic disks \begin{equation}\label{eq-poisson-vertical-phantomdensity} 4\pi\,G\,\left[\rho(R,z)-\rho_\mathrm{RC}(R)\right] = \frac{\partial^2 \Phi}{\partial z^2}\,. \end{equation} We can also write the phantom density in terms of the Oort constants \begin{equation}\label{eq-phantomdens-oort} \rho_\mathrm{RC}(R) = \frac{(B^2-A^2)}{2\pi\,G}\,. \end{equation}
As we did for the distribution function in the disk mid-plane in the first part of this chapter, we start by discussing the axisymmetric, vertical Jeans equation in more detail (including its non-decoupled form of Equation 10.4) before going on to full phase-space distribution function models.
10.4.1. The vertical Jeans equation¶
Many analyses of the vertical kinematics in galactic disks—most productively done in the solar neighborhood—make use of the vertical Jeans equation. We can re-write Equation (10.4) to provide the gravitational force \(-\frac{\partial \Phi}{\partial z}\) in terms of the density and velocity dispersions (we substitute \(\sigma_z^2 = \overline{v_z^2}\) and \(\sigma_{Rz}^2 = \overline{v_R\,v_z}\), because in an equilibrium, axisymmetric system, \(\overline{v_R} = \overline{v_z} = 0\)) \begin{equation}\label{eq-jeans-vertical-force} -\frac{\partial \Phi}{\partial z} = \frac{1}{\nu}\,\frac{\partial [\nu\,\sigma_z^2]}{\partial z} +\frac{1}{R\,\nu}\,\frac{\partial [R\,\nu\,\sigma^2_{Rz}]}{\partial R} \,. \end{equation} Given observations at a given \(R\) of the tracer-density profile \(\nu(z)\) and the velocity-dispersion profile \(\sigma_z(z)\), we can directly determine the vertical component of the gravitational field \(g_z(z;R) = -\frac{\partial \Phi}{\partial z}\) at \(R\), but this further requires knowledge of \(\partial [R\,\nu\,\sigma^2_{Rz}]/\partial R\). This latter information has historically been difficult to obtain directly (although with Gaia data it should be possible to measure it directly as well) and the typical approach has been to make assumptions about it. This term is generally known as the tilt of the velocity ellipsoid, because when we consider \(\sigma^2_{Rz}\) as an entry in the velocity dispersion tensor of Equation (10.31), it can be equivalently be parameterized as an angle \(\alpha\) of the angle between the velocity’s ellipsoid and the \(z\) axis: \begin{equation}\label{eq-diskequil-tilt} \tan \left( 2\,\alpha\right) = 2\,\frac{\sigma^2_{Rz}}{\sigma_R^2-\sigma_z^2}\,. \end{equation}
One assumption about the tilt of the velocity ellipsoid that we have already used many times is that the vertical motion is decoupled from the planar motion, because then \(\sigma^2_{Rz} = 0\) and, thus, \(\alpha = 0\) and we are left with the decoupled vertical Jeans equation (Equation 10.6). Another assumption, more appropriate for non-disk orbits is that on average stars move in a spherical potential. In that case the velocity ellipsoid “points towards the Galactic center” at all heights and, thus, \(\tan \alpha = z/R\). “Points towards the Galactic center” here means that the velocity ellipsoid tensor is aligned—that is, diagonal—in spherical coordinates, which is the case for all spherical distribution functions that we discussed in Chapter 5.6, including those with non-zero orbital anisotropy (which only affects the relative magnitude of the diagonal elements). Intermediate to these possibilities is that the motion decouples in a set of spheroidal components, e.g., in confocal prolate coordinates with foci at \((R,z) = (0,\pm \Delta)\) for some constant \(\Delta\) (e.g., de Zeeuw 1985; Binney 2012a; see Chapters 9.4.3 and 12 for more discussion of this coordinate system); then the velocity ellipsoid will be aligned with the coordinate axes in the spheroidal coordinate system, which can be chosen to be intermediate between \(\alpha = 0\) and \(\tan \alpha = z/R\). Of course, the velocity ellipsoid does not have to be globally diagonal (that is, at all positions) in any coordinate system!
While the tilt term is an unknown quantity that one needs to make assumptions about, even in the extreme case where the velocity dispersion tensor points to the Galactic center, the tilt term in Equation (10.38) is smaller by a factor of about a hundred—for solar-neighborhood populations—than the first term on the right-hand side in Equation (10.38) at \(|z| \lesssim 1\,\mathrm{kpc}\) (Zhang et al. 2013), and it can therefore be largely ignored when analyzing data close to the Galactic mid-plane. This is again a statement about the fact that the vertical motion approximately decouples from the planar motion, which is an especially good assumption to make about distributions of orbits.
We can combine the vertical Jeans equation with the Poisson equation to directly relate the mass distribution to the observed density and velocity dispersion. First, we integrate Equation (10.35) to obtain a version of the Poisson equation that relates \(\Sigma(z;R)\), the surface density between \(-z\) and \(z\)—which we will refer to as the surface density up to height \(z\)—to the gravitational potential \begin{equation}\label{eq-surfdens-frompoisson} \Sigma(z;R) = \frac{1}{2\pi\,G}\left[\frac{\partial \Phi}{\partial z}+\frac{1}{R}\,\int_0^\infty \mathrm{d}\,z \frac{\partial}{\partial R}\left(R\,\frac{\partial \Phi}{\partial R}\right) \right]\,, \end{equation} where we have assumed that the mass distribution is symmetric for \(z \rightarrow -z\). Substituting \(\partial \Phi / \partial z\) from Equation (10.38) and using the approximate, constant, form of the integrand from Equation (10.37), we find \begin{equation}\label{eq-surfdens-fromverticaljeans} \Sigma(z;R) = \frac{1}{2\pi\,G}\left[z\,(B^2-A^2) -\frac{1}{\nu}\,\frac{\partial [\nu\,\sigma_z^2]}{\partial z} -\frac{1}{R\,\nu}\,\frac{\partial [R\,\nu\,\sigma^2_{Rz}]}{\partial R} \right]\,. \end{equation} This equation demonstrates that we rather directly constrain the surface density up to height \(z\) when we measure the stellar density profile \(\nu(z)\) and the kinematics around height \(z\). We will discuss applications of the vertical Jeans equation to the kinematics in the solar neighborhood in Section 10.4.4 below.
10.4.2. The vertical equilibrium of a self-gravitating disk¶
As a first set of solutions of Equation (10.34), we consider distribution functions of the form \begin{equation}\label{eq-diskequil-vertical-isothermal-df} f(E_z) = \frac{\rho_0}{\sqrt{2\,\pi}\sigma_z}\,e^{-\frac{E_z}{\sigma_z^2}}\,. \end{equation} This is simply the one-dimensional version of the isothermal sphere that we investigated in Chapter 5.6.2 and it is also similar to all of the razor-thin disk distributions that we considered above (which all become exponentials of minus the epicycle energy for nearly circular orbits). Like the isothermal sphere, the velocity distribution of this distribution function is Gaussian at all \(z\): \(f(v_z|z) = \exp\left[-v^2_z/(2\sigma_z^2)\right]/(\sqrt{2\,\pi}\sigma_z)\). The density is an exponential of minus the potential \(\nu(z) = \rho_0\,\exp\left[-\Phi_z(z)/\sigma_z^2\right]\). These results are valid for any isothermal distribution function in a given potential \(\Phi_z(z)\).
If we also require self-consistency—that the potential is sourced by the density implied by the distribution function—we have an additional constraint from the Poisson equation, which in one dimension is \(\mathrm{d}^2\Phi_z/\mathrm{d} z^2 = 4\pi G \rho(z)\), where \(\rho(z) = \nu(z)\) given above. A self-consistent, isothermal galactic disk therefore satisfies (Spitzer 1942; Camm 1950) \begin{equation} \frac{\mathrm{d}^2\Phi_z}{\mathrm{d} z^2} = 4\pi\,G\,\rho_0\,e^{-\frac{\Phi_z(z)}{\sigma^2_z}}\,. \end{equation} This equation is solved by the following potential–density pair \begin{align}\label{eq-diskequil-vertical-isothermal-df-sol} \Phi_z(z) & = 2\,\sigma^2\,\ln\left(\cosh\left[\frac{z}{2\,H}\right]\right)\,;\quad \rho(z) = \rho_0\,\mathrm{sech}^2\left[\frac{z}{2\,H}\right]\,, \end{align} where \(H^2 = \sigma^2/[8\pi\,G\,\rho_0]\) or, alternatively, \(H = \sigma^2/[2\pi\,G\,\Sigma]\), where \(\Sigma = 4\,\rho_0\,H\) is the total surface density. This is the self-gravitating, isothermal sheet (“sheet”, because the decoupled vertical dynamics in a disk is that of sheets; Cuperman et al. 1969; Schulz et al. 2013).
10.4.3. The vertical distribution function for a given density profile¶
Similar to what we did for spherical ergodic distribution functions in Chapter 5.6.1, we can ask what the equilibrium vertical distribution function \(f(E_z)\) for a population with a given density \(\nu(z)\) orbiting in a vertically-decoupled gravitational field specified by the potential \(\Phi_z(z)\) is. Using a procedure analogous to that followed in Chapter 5.6.1, we determine this equilibrium distribution function here.
The density \(\nu(z)\) is given by the integral of the distribution function over velocity \begin{align} \nu(z) & = \int_{-\infty}^\infty \mathrm{d} v_z\,f(E_z[z,v_z]) = 2\,\int_{\Phi_z(z)}^\infty \mathrm{d} E_z\,\frac{f(E_z)}{\sqrt{2\,\left[E_z-\Phi_z(z)\right]}}\,.\label{eq-vertdens-from-fEz} \end{align} Like for a spherical potential, for a one-dimensional potential, we can invert the relation \(\Phi_z(z)\) (at least at \(z > 0\); because we assume that the disk is symmetric around the mid-plane, \(\Phi_z(z) = \Psi\) has two solutions, one at \(z_\Psi\) and one at \(-z_\Psi\)) and we can write the density as a function of \(\Phi_z\) instead \begin{align} \nu(\Phi_z) & = 2\,\int_{\Phi_z}^\infty \mathrm{d} E_z\,\frac{f(E_z)}{\sqrt{2\,\left[E_z-\Phi_z\right]}}\,. \end{align} This is an Abel integral equation, which can be inverted as (see Appendix B.4.1) \begin{align}\label{eq-verticaldf-fordens} f(E_z) & = \frac{1}{\pi}\,\int_{E_z}^\infty \mathrm{d} \Phi_z\,\frac{-\mathrm{d} \nu / \mathrm{d} \Phi_z}{\sqrt{2\,\left[\Phi_z-E_z\right]}}\,. \end{align}
The distribution function obtained using Equation (10.47) is the unique equilibrium distribution function for a given density \(\nu\) in a given potential \(\Phi_z\). If we have a well-measured density profile \(\nu(z)\) of a population of stars in the solar neighborhood, we can use Equation (10.47) to determine the equilibrium distribution function for different potentials and compare the velocity distribution that these distribution functions predict with the observed kinematics to find the best matching potential.
10.4.4. The vertical equilibrium in the solar neighborhood¶
10.4.4.1. The local density of matter¶
We can roughly separate the types of analyses of the vertical density and kinematics in the solar neighborhood into two main classes: those that look at stars at \(|z| \ll z_d\), that is, less than the (mass-weighted) scale height of the stellar disk (\(z_d \approx 400\,\mathrm{pc}\); Bovy et al. 2012) and those that look at stars with larger vertical excursions. In the first type, we can approximate the vertical density as being approximately constant \(\rho(z) \approx \rho_0 = \mathrm{constant}\); this type of analysis is known as the “Oort limit”, after Oort who was the first to perform this type of analysis in Oort (1932). Under this assumption, the Poisson Equation (10.35) is solved by the potential \begin{equation} \Phi_z(z) = \frac{\omega^2\,z^2}{2}\,, \end{equation} where \(\omega^2 = 4\pi\,G\,[\rho_0+\rho_\mathrm{RC}(R)]\), including a possible contribution from the phantom density for a non-flat rotation curve (see Equation 10.36). A possible linear term in \(z\) in \(\Phi_z(z)\) must be zero if the potential is symmetric around \(z=0\) and we have fixed the constant such that \(\Phi_z(0) = 0\). Thus, close to the plane, the gravitational potential is approximately that of a harmonic oscillator centered on \(z=0\).
More generally, we can measure \(\Sigma(z;R)\) using the Jeans-equation method from Equation (10.41). At small \(z\) where the density is approximately constant, \(\Sigma(z;R) = 2\,\rho_0\,z\) and we can thus obtain the local density from the slope of \(\Sigma(z;R)\). If the rotation curve is flat, \(\Sigma(z;R) = -g_z(|z|)/[2\pi\,G]\) and then we can obtain the local density from the slope of the vertical gravitational field \(g_z(z)\) with \(z\).
Analyses of the vertical kinematics of this form have a long and venerable history. We will only discuss some highlights of this history here. The first analysis of this type was done by Oort (1932). This paper was also the first to discuss “dark matter” as a missing mass to account for the discrepancy between the amount of mass inferred from star light and that inferred from dynamics (Zwicky’s paper on the Coma cluster only appeared a year later). Oort (1932) used the vertical Jeans equation in the form of Equation (10.38) with zero tilt (that is, without the second term on the right-hand side; his Equation 9) to determine the vertical field (or acceleration; \(K\) in his notation) \(g_z(z) = -\frac{\partial \Phi}{\partial z}\) from observations of \(\nu(z)\) (which he called \(\Delta\)) and \(\sigma_z^2\) (which he called \(\overline{Z^2}\)) of local stars. His measurement is displayed in his Figure 4, reproduced here in Figure 10.11.
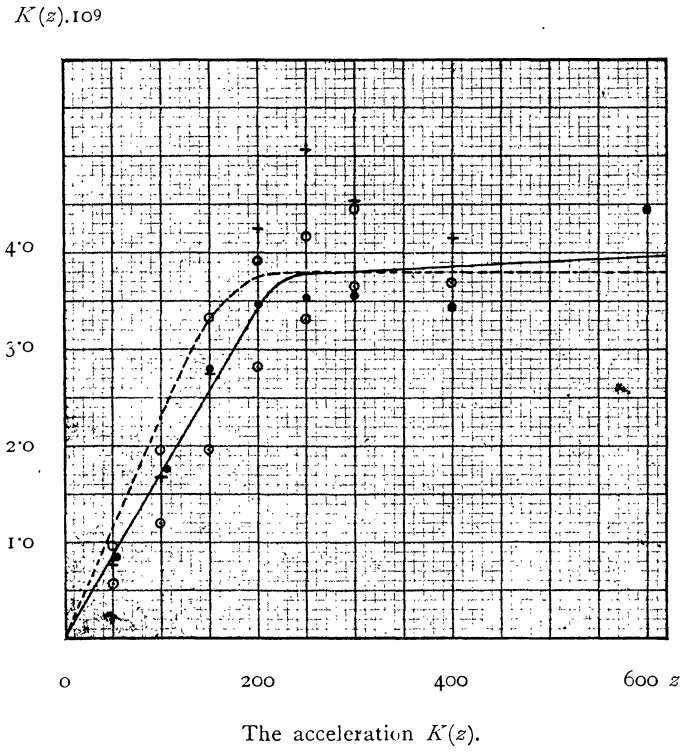
Figure 10.11: Vertical force as a function of height (Oort 1932).
The horizontal axis shows the vertical height \(z\) in pc, while the vertical axis shows \(g_z\) in units of \(10^{-9}\,\mathrm{cm\,s}^{-2}\). To be able to quickly interpret the measurements in this and the next section, the following unit conversions are useful \begin{align} 10^{-9}\,\mathrm{cm\,s}^{-2} &\approx 0.3\,\left(\mathrm{km\,s}^{-1}\right)^2\,\mathrm{pc}^{-1}\,;\quad \left(\mathrm{km\,s}^{-1}\right)^2\,\mathrm{pc}^{-1}/[2\pi\,G] \approx 37\,M_\odot\,\mathrm{pc}^{-2}\,. \end{align} We can thus directly read off Oort’s measurement of the local density \(\rho_0\) (assuming a flat rotation curve, so no phantom density) from his measurement of \(g_z(z)\) (using the point at \(z=200\,\mathrm{pc}\) to estimate the slope): \begin{equation} \rho_0 \approx (3.5\times10^{-9}\,\mathrm{cm\,s}^{-2}/[200\,\mathrm{pc}]/2) \approx 0.1\,M_\odot\,\mathrm{pc}^{-3}\,. \end{equation} This value is in fact still the accepted value, as we will see below. Oort (1932) compared this value to his best estimate of visible matter, which was \(\rho_{\mathrm{vis}} \approx 0.04\,M_\odot\,\mathrm{pc}^{-3}\) and invoked “dark matter” to explain the discrepancy between the two. While this is (arguably, as with all things) the first use of “dark matter” to explain the discrepancy between mass-to-light-ratio-estimated mass and dynamically-estimated mass, Oort was well aware of the fact that this missing mass was most likely made up of (i) numerous faint stars below the detection limit and (ii) interstellar gas. Current inventories of the solar neighborhood indeed show that all of the \(\rho_0 = 0.1\,M_\odot\,\mathrm{pc}^{-3}\) local density is accounted for by stars and gas (with just enough uncertainty to allow for the small amount of halo dark matter; McKee et al. 2015; Bovy 2017b).
This type of analysis was refined over the next decades by, for example, Oort (1960), Bahcall (1984), and Kuijken & Gilmore (1989b). Unfortunately, these analyses gave very different results for \(\rho_0\), with some returning a value that is twice the value from Oort (1932). If this were the correct value, then there would be a large amount of true dark matter contained in the disk of the Milky Way.
Like for the local planar velocity distribution, the Hipparcos data provided a superior data set to investigate the vertical kinematics of stars in the solar neighborhood. Holmberg & Flynn (2000) used the Hipparcos data to determine the local density from the kinematics and density distribution of A and F-type stars, which have vertical excursions \(\ll z_d\). Their method differs from that used by Oort above in that they use the full distribution function to constrain the potential, rather than just the zero-th and second moment in the Jeans equations. Specifically, for both populations of stars they use (i) observations of the velocity distribution \(f(v_z|z=0)\) at \(z=0\) and (ii) observations of the vertical density profile \(\nu(z)\). The velocity distribution does not depend on the gravitational potential, but combined with a gravitational potential can predict \(\nu(z)\). This prediction, for different \(\Phi_z(z)\) can then be compared to the observed density profile and the best \(\Phi_z(z)\) is that that provides the best match to the density profile. Their potential model is rather complicated: it is the sum of potentials contributed by different stellar populations and different gas components, but the only free parameter they consider is an overall amplitude parameter that increases or decreases the contribution from all components in lockstep. This amplitude parameter can be straightforwardly converted to the local density \(\rho_0\) in their model.
Equation (10.45) shows how we can determine \(\nu(z)\) from \(f(E_z)\) and a potential model \(\Phi_z(z)\). We can use the observed velocity distribution \(f(v_z)\) to obtain \(f(E_z)\), because the potential is zero and \(E_z = v_z^2/2\) at \(z=0\); therefore \(f(E_z|z=0) = f(v_z|z=0)\). We can then re-write Equation (10.45) as \begin{equation}\label{eq-vertdens_fromfvz0} \nu(z) = 2\,\int_{\sqrt{2\,\Phi_z(z)}}^\infty \mathrm{d} v_z\,\frac{v_z\,f(v_z|z=0)}{\sqrt{v_z^2-2\,\Phi_z(z)}}\,. \end{equation} This equation makes sense. For an equilibrium disk, all stars pass through the \(z = 0\) mid-plane. Only stars in the mid-plane with \(|v_z| > \sqrt{2\,\Phi_z(z)}\) will travel to height \(z\), otherwise their energy is too low to travel to this height; therefore we only integrate over \(v_z > \sqrt{2\,\Phi_z(z)}\) to determine \(\nu(z)\). The stars that have just enough energy to make it to a given height spend the most time there, because stars slow down near their turning point; this leads to the \(v_z/\sqrt{v_z^2-2\,\Phi_z(z)}\) weighting, which (integrably) diverges at \(v_z^2 = 2\,\Phi_z(z)\) and declines for larger \(v_z\).
The equilibrium dynamical model does a good job of fitting the density distribution and Holmberg & Flynn (2000) find the best-fitting \begin{equation}\label{eq-diskequil-local-midplane-density} \rho_0 = 0.102\pm0.010\,M_\odot\,\mathrm{pc}^{-3}\,. \end{equation} Because the existence of a \(\approx10\%\) vertical phase-space spiral systematically limits equilibrium-analyses such as those described here and in the next subsection at the 10% level (see the discussion of Figure 10.10 in Chapter 10.3.2), Gaia data has not improved these measurements of \(\rho_0\). To do better, it is necessary to account for the non-equilibrium vertical dynamics. But doing that, there currently remain large discrepancies between different measurements (e.g., Widmark et al. 2021; Guo et al. 2023) and the measurement in Equation (10.52) remains a good value to use.
It is interesting at this point to contrast the two types of analyses that we discussed in this section. In a Jeans analysis, we constrain the gravitational force from observations of the density, velocity dispersion, and their gradients at the position where we constrain the force. Thus, the Jeans equations provide constraints on the gravitational potential at the same location as the measurements. In contrast, using the full distribution function, we can use observations of the distribution function at one location, to constrain the gravitational potential over a much larger volume. Equation (10.51) demonstrates that we can constrain the gravitational potential over the entire volume covered by the orbits whose velocity distribution we observe at the mid-plane. This is the case as long as we have measurements of the density throughout this volume, but we do not require kinematics throughout the volume, unlike when using the Jeans equation. Thus, using the full distribution function is more powerful than using the Jeans equation. This is generally the case.
10.4.4.2. The local surface density of matter and the local dark-matter density¶
When we measure the vertical density and kinematics of stars at larger distances from the Milky-Way mid-plane (\(z \gtrsim z_d\)), the gravitational force (e.g., determined using the vertical Jeans equation) most directly measures the surface density because of Equation (10.40). If we can measure how the surface density depends on height from \(z \approx z_d \approx 400\,\mathrm{pc}\) to \(z \gtrsim 1\,\mathrm{kpc}\), we can decompose the surface density into the contribution from the disk and that from the dark-matter halo. This is because the contribution from the disk saturates at \(z \gtrsim z_d\). The contribution to the density from the dark-matter halo is roughly constant (because the halo density only has gradients on scales \(\approx R \gg z_d\) near the Sun) and therefore provides a constant increase of \(\Sigma(z;R)\). Thus, in a simple model of a vertically-exponential disk plus a constant-density dark matter halo, the surface density is \begin{equation}\label{eq-surfdens-decompose-disk-halo} \Sigma(z;R) = \Sigma_d(R)\,\left(1-e^{-z/z_d}\right) + 2\,\rho_\mathrm{DM}(R)\,z\,, \end{equation} where \(\Sigma_d(R)\) is the total surface density of the disk at radius \(R\) and \(\rho_\mathrm{DM}(R)\) is the local dark-matter density. Measurements of the density and kinematics of stars between \(z_d \lesssim z \lesssim \mathrm{few}\times z_d\) can therefore constrain the main parameters of this simple model: \(\Sigma_d(R)\), \(z_d\), and \(\rho_\mathrm{DM}(R)\).
A pioneering analysis of this type was done by Kuijken & Gilmore (1989a). They determined the density and kinematics of a sample of K dwarfs toward the South Galactic Pole and fit it by predicting the velocity distribution from the observed density distribution using Equation (10.47) for different potentials. They predict the full velocity distribution, use it to compute the probability of the data for different models of the potential, and maximize the probability to find the best potential. Because their data set was small, Kuijken & Gilmore (1989a) added an additional constraint to their model to also match the rotation curve using the same disk-plus-halo model that they used (this constraint goes beyond using the slope of the rotation curve to determine the phantom density in Equation 10.37). Because their data was mostly around \(z \approx 1.1\,\mathrm{kpc}\), they found that they could not unambiguously decompose \(\Sigma(z;R)\) into the disk and halo components (like in Equation 10.53, but they used a different model decomposition), but instead best measured the surface density at the typical height of their sample: \(\Sigma(z=1.1\,\mathrm{kpc};R)\) (as expected from Equation 10.40). For this they found (Kuijken & Gilmore 1991): \begin{equation} \Sigma(z=1.1\,\mathrm{kpc};R_0) = 71\pm6\,M_\odot\,\mathrm{pc}^{-2}\,. \end{equation} This is still often used as a constraint on the local mass distribution, even though it has been refined by more recent analyses. Because they could not unambiguously decompose the surface density into disk and halo, they did not directly measure \(\rho_\mathrm{DM}(R_0)\) .
Because stars at large distances \(z \approx 1\,\mathrm{kpc}\) with accurate distances and velocities are required to measure \(\Sigma(z;R)\) from the vertical dynamics, for a long time the Kuijken & Gilmore (1989a) constraint remained the best measurement. This has changed during the last decade, due to the appearance of large spectroscopic surveys that contain large samples of disk stars around \(z \approx 1\,\mathrm{kpc}\) for which accurate distances can be obtained from the precise photometry provided by large photometric surveys (e.g., SDSS/SEGUE; Yanny et al. 2009). Better measurements of the dark-matter density can be obtained by observing the kinematics of stars at \(z \gtrsim 1.5\,\mathrm{kpc}\), because at these heights the only increase in the surface density comes from the dark-matter density (the disk density is essentially zero at such large heights above the mid-plane). However, such measurements are difficult to obtain. An analysis of this type was performed by Bovy & Tremaine (2012), who used measurements of the kinematics of red giants from Moni Bidin et al. (2012) to determine \(\Sigma(z;R_0)\) at \(1.5\,\mathrm{kpc}\lesssim z \lesssim 4.5\,\mathrm{kpc}\) using the Jeans Equation (10.38) including the tilt term (which was also measured from the kinematics), assuming \(\nu(z) \propto e^{-|z|/[900\,\mathrm{pc}]}\) because the density was not directly measured (this assumption only has s small effect on the results, because the scale height realistically cannot be much larger or smaller than 900 pc). The measured \(\Sigma(z;R)\) in Figure 10.12 clearly displays the expected linear trend with height expected if the only contribution to the density is a constant dark-matter halo density:

Figure 10.12: Dynamically-determined surface density as a function of height at the solar circle (Bovy & Tremaine 2012).
The solid line with error bars is the main result (the lower solid line labeled as “incorrect” shows the result of making an incorrect assumption about the asymmetric drift, which was made in the original analysis of these data). The linear slope gives a measurement of the local dark matter density of \begin{equation} \rho_\mathrm{DM} = 0.008\pm 0.003\,M_\odot\,\mathrm{pc}^{-3}\,. \end{equation} At the time, this was the first high-confidence determination of the local dark-matter density.
In this section, we have focused on analyses that either assume that the vertical kinematics is decoupled from the planar kinematics or take into account the coupling using the tilt term in the vertical Jeans equation. More sophisticated analyses have been performed by Bovy & Rix (2013) (of the SDSS/SEGUE data), Piffl et al. (2014) (of RAVE data; Steinmetz et al. 2006), and Binney & Vasiliev (2023) (of Gaia line-of-sight velocity data; Katz et al. 2019). These papers use equilibrium distribution models that are functions of three integrals of the motion (the actions, computed using the method from Chapter 9.4.3) and these models properly take into account the coupling between the vertical and planar motions. Further information on these types of models can be found in Binney (2010), Binney & McMillan (2011), Binney (2012b), and Binney & Vasiliev (2023).

